TensorFlow学习笔记(三)

Posted on | In , , |
深层神经网络

TensorFlow学习笔记(三)

激活函数

在存在的数据集中有些数据可以简单的用一条直线或者一个平面来划分数据，则称这些为线性可分。但是有些数据是不可以分的，这样就没有办法用一条直线或者平面来区分数据。

这时候可以通过激活函数(Activation function)入一个非线性的激活函数增加模型的表达能力。

常见的激活函数有

  • sigmoid

$$
sigmoid(x)=\frac{1}{1+e^{-x}}
$$

cs231n中提到这个一些缺点:
会产生梯度消失、不关于原点中心对称会导致$f(\sigma{w_ix_i+b})$中的梯度恒正或恒负收敛速度慢、计算耗时

  • tanh

$$
tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}
$$

这里只解决了sigmoid中的不对称的问题、通常情况下能用tanh就不采用sigmoid。

  • ReLU

$$
ReLU(x)=\begin{cases}
0& \text{x ≥ 0}\
x& \text{x < 0}
\end{cases}
$$

这个是最常用的一个激活函数
优点: 收敛比较之前的激活函数会加速6倍左右、在正数范围内不会发生梯度消失、计算速度快
缺点: 不关于0中心对称、x<0时梯度消失、0点梯度未定义
初始化时,ReLU神经元将偏置值设为很小的正数(eg.0.0001)而不是0

  • 下面这几个都是ReLU的变体

  • Leaky ReLU

$$
f(x)=max(0.01x,x)
$$

  • PReLU

$$
f(x)=max(\alpha x,x)
$$

  • ELU

$$
f(x)=\begin{cases}
x& \text{x>0}\
\alpha(e^{x}-1)& \text{x ≤ 0}
\end{cases}
$$

  • Maxout

$$
f(x)=max(w^{T}{1}x+b_1,w^{T}{2}x+b_2)
$$

损失函数

cs231n Loss functions这里有损失函数的详细解释

之前介绍的只是对于二分类的网络处理。虽然可以设置多个阈值来实现多分类但是实际解决问题不会这么处理。这样就可以应用损失函数解决多分类问题。

假设神经网络以一个n维数组作为输出结果，假设以识别手写体的数字1为例，则输出结果越接近[0,1,0,0,0,0,0,0,0,0]越好，评估训练得到的向量与这个准确的实际的向量的方法最常采用交叉熵(cross entropy)的评估方法。

如果给出2个概率分布p,q 通过q来表示p的交叉熵为:

$$
H(p,q)=-\Sigma{p(x)\log{q(x)}}\
p:true lable\
q:prediction
$$

交叉熵刻画的是两个概率分布之间的距离,然而神经网络的输出不一定是一个概率分布，这时就需要某种方法将神经网络前向传播的结果变成概率分布。softmax回归(softmax regression)是最常用的方法。

假设神经网络的输出为$y_1,y_2 \cdots y_n$，那么经过softmax回归之后得到的输出为:

$$
softmax(y_i)=\frac{e^{y_i}}{\Sigma^n_{j=1}{e^{y_j}}}
$$

  • 在TensorFlow中提供了交叉熵和softmax回归的函数
1
2
# 一般都交叉熵会与softmax一起使用:
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=y_)
  • 如果解决的不是分类问题，而是预测房价什么的输出是一个实数，这时最常用的是均方误差(MSE,mean squared error)

$$
MSE(y,y’)=\frac{\Sigma^n_{i=1}{(y_i-y’_i)}^2}{n}\
y_i是第i个数据正确答案,y’_i是数据网络的预测值。
$$

1
mse = tf.reduce_mean(tf.square(y_ - y))

神经网络优化算法

梯度下降算法Gradient Descent

  • Gradient Descent (GD)

$$
\theta_i :=\theta_i-\alpha\frac{\partial}{\partial \theta_i}J(\theta)
$$

$$
\begin {aligned}
\frac{\partial}{\partial \theta_i}J(\theta) &= \frac{\partial}{\partial \theta_i}{\frac{1}{2}}{(h_\theta(x)-y)^2} \
&=(h_\theta(x)-y) \frac{\partial}{\partial \theta_i}(\theta_0x_0+\cdots+\theta_nx_n-y) \
&=(h_\theta(x)-y)x_i
\end {aligned} \
$$

所以$\theta_i:=\theta_i-\alpha(h_\theta(x)-y)x_i$,其中$\alpha$为学习速率

性质: 一定会结束,取决于初始值,局部最小值梯度为0. 来自Andrew Ng: Stanford Machine Learning

  • Batch Gradient Descent

$$
\theta_i:=\theta_i-\alpha\sum_{j=1}^n (h_\theta(x^{(j)})-y^{(j)})x_i^{(j)}
$$

遍历所有数据,适用于较小数据

  • Stochastic Gradient Descent (SGD)

执行此算法时,每次不一定按照局部最小值方向前行,最终在局部最小值附近。

  • 还有一种利用矩阵运算的方法求得$J(\theta)$的最小值

$$
\theta = (x^Tx)^{-1}x^Ty
$$

直接给出结论,推导过程较长,这里不写了。。具体可以参考Ng的机器学习课程中有具体推导见 Andrew Ng: Stanford Machine Learning

更多的优化算法的具体情况可以看cs231n

cs231n有两张图提供了对比

在TensorFlow中的优化算法

在官方的API文档中有专门的一节给出优化算法的API: Gating Gradients

  • 常用的有:
  1. tf.train.AdagradOptimizer
  2. tf.train.MomentumOptimizer
  3. tf.train.AdamOptimizer

学习率的设置

学习率决定了参数每次更新的幅度,如果幅度过大,那么可能导致参数在极优值的两侧来回移动。
学习率过大过小都可能导致不理想的优化效果,参数过大可能导致不在最小值收敛,参数过小虽然能保证收敛,但可能会大大降低优化速度。

TensorFlow提供了一个指数衰减的学习速率tf.train.exponential_decay,通过这个函数可以先使用较大的学习率来快速得到较优解,然后随着迭代的继续减小学习率,是的模型在训练后期更加稳定。

1
decayed_learning_rate = learning_rate * decay_rate ^ (global_step /decay_steps)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
# 实际的程序代码:
global_step = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
    0.1, global_step, 100, 0.96, staircase=True)
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(
    cross_entropy, global_step=global_step)

'''
以之前的二分类程序为例,把原来的学习率和改成指数衰减的形式。
得到如下结果
After 0 trainning steps,cross entropy on all data is 0.00922738
After 1000 trainning steps,cross entropy on all data is 0.0072059
After 2000 trainning steps,cross entropy on all data is 0.00654774
After 3000 trainning steps,cross entropy on all data is 0.00614149
After 4000 trainning steps,cross entropy on all data is 0.00588985
'''

# 完整程序如下:
import tensorflow as tf
from numpy.random import RandomState
# 训练数据batch大小
batch_size = 8
# 定义神经网络的参数
weights1 = tf.Variable(tf.truncated_normal([2, 3], stddev=2, seed=1))
weights2 = tf.Variable(tf.truncated_normal([3, 1], stddev=2, seed=1))
# 这里None是方便改变batch大小,训练时把数据分成较小的batch,测试使用全部数据
# 当数据集较小时这样容易测试,但数据集较大时,将大量数据放入一个batch
x = tf.placeholder(tf.float32, shape=(None, 2), name="x-input")
y_ = tf.placeholder(tf.float32, shape=(None, 1), name="y-input")

a = tf.matmul(x, weights1)
y = tf.matmul(a, weights2)

cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
# learning_rate = 0.1
global_step = tf.Variable(0)
learning_rate = tf.train.exponential_decay(
    0.1, global_step, 100, 0.96, staircase=True)
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(
    cross_entropy, global_step=global_step)

# train_step = tf.train.AdamOptimizer(learning_rate).minimize(
#     cross_entropy)

# 随机模拟数据集
rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size, 2)
# 这里用x1+x2<1表示为正样本(1),其他为负样本(0)
Y = [[int(x1 + x2 < 1)] for (x1, x2) in X]

with tf.Session() as sess:
    init_w = tf.global_variables_initializer()
    sess.run(init_w)
    print(sess.run(weights1))
    print(sess.run(weights2))

    # 训练轮数
    step = 5000
    for i in range(step):
        # 每次选取batch_size个样本进行训练
        start = (i * batch_size) % dataset_size
        end = min(start + batch_size, dataset_size)
        # 对选取的样本训练神经网络并更新参数
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        # 每隔1000次 将输出所有数据的交叉熵。
        if i % 1000 == 0:
            total_cross_entropy = sess.run(cross_entropy,
                                           feed_dict={x: X,
                                                      y_: Y})
            print("After %d trainning steps,cross entropy on all data is %g" %
                  (i, total_cross_entropy))

    # 在训练之后输出神经网络的值
    print(sess.run(weights1))
    print(sess.run(weights2))

过拟合问题

在真是的应用中,常常会遇到模型模拟了训练数据,而我们的目标确实让模型去对未知的数据做出判断。所谓过拟合是指当模型过于复杂之后,它会”记住”每个训练数据。如果模型的参数比训练的总数据还多,会导致损失函数最终为0。这种情况虽然对训练集的拟合较好,但是对于验证集则很差。

正则化

为了避免过拟合的问题,一个最常用的方法是正则化(regularization)。正则化是在损失函数中加入刻画模型复杂程度的指标。假设刻画模型在训练数据上的表现的损失函数为$J(\theta)$,那么优化时,不直接优化$J(\theta)$,而是优化$J(\theta)+\lambda R(w)$。其中$R(w)$刻画的是模型的复杂程度,而$\lambda$表示模型复杂损失在总损失中的比例。
这里$\theta$表示神经网络中所有的参数,包括边上的权重w和偏置b。一般来说模型复杂度只由权重w决定。常用的刻画模型复杂度的函数$R(w)$有两种。

cs231n里有正则化的详细介绍

  • L1正则化(L1 Regularization)

$$\sum_k \sum_l (w_{k,l})$$

  • L2正则化(L2 Regularization)也称Ridge(岭回归)

$$\sum_k \sum_l (w_{k,l})^2$$

L0正则化的值是模型参数中非零参数的个数。
L1正则化表示各个参数绝对值之和。
L2正则化标识各个参数的平方的和的开方值。
可能这些公式不同的地方公式会不同,我用的是cs231n课程中的写法,但都表示同一个意思。

还有一些可能会用到的

  • Elastic Net 这是一种可以看出L1+L2的合成。

$$R(w)=\sum_k \sum_l \beta w_{k,l}^2+|w_{k,l}|$$

  • Max norm constraints 类似于限制每个神经元w的最大值。论文

Max norm constraints. Another form of regularization is to enforce an absolute upper bound on the magnitude of the weight vector for every neuron and use projected gradient descent to enforce the constraint. In practice, this corresponds to performing the parameter update as normal, and then enforcing the constraint by clamping the weight vector $\vec{w}$ of every neuron to satisfy $\Vert \vec{w} \Vert_2 < c$are on orders of c 3 or 4. Some people report improvements when using this form of regularization. One of its appealing properties is that network cannot “explode” even when the learning rates are set too high because the updates are always bounded.

  • Dropout 随机失活一部分神经元

cs231n中提到的正则化

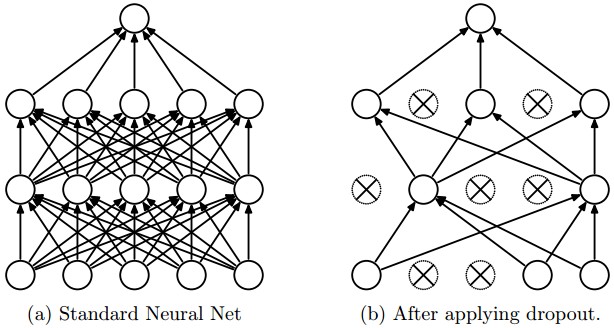
  • 在TensorFlow中提供了带正则化的损失函数:
1
2
3
4
5
6
7
8
9
10
11
12
# 这是正则化函数的定义
import tensorflow as tf
w = tf.Variable(tf.random_normal([2, 1]), stddev=1, seed=1)
y = tf.matmul(x, w)
loss = tf.reduce_mean(tf.squre(y_ - y)) + tf.contrib.layers.l2_regularizer(lambda)(w)

'''
其中loss为定义的损失函数,第一个部分是均方误差损失函数，第二个部分是正则化。
lambda参数表示正则化项的权重，w是计算正则化损失的参数。
TensorFlow提供了tf.contrib.layers.l2_regularizer函数,他可以返回一个函数，
这个函数计算给定参数的L2正则化值，类似的还有tf.contrib.layers.l1_regularizer
'''
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 这里是使用L1、L2正则化的实例
import tensorflow as tf
weights = tf.constant([[1.0, -2.0], [-3.0, 4.0]])
with tf.Session() as sess:
    print(sess.run(tf.contrib.layers.l1_regularizer(0.5)(weights))) # 0.5是正则化项的权重
    print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(weights))) # l2时TensorFlow会除以2,使得求导结果简洁

'''
# 输出
W tensorflow/core/platform/cpu_feature_guard.cc:45] The TensorFlow library wasn't compiled to use SSE4.1 instructions, but these are available on your machine and could speed up CPU computations.
W tensorflow/core/platform/cpu_feature_guard.cc:45] The TensorFlow library wasn't compiled to use SSE4.2 instructions, but these are available on your machine and could speed up CPU computations.
W tensorflow/core/platform/cpu_feature_guard.cc:45] The TensorFlow library wasn't compiled to use AVX instructions, but these are available on your machine and could speed up CPU computations.
W tensorflow/core/platform/cpu_feature_guard.cc:45] The TensorFlow library wasn't compiled to use AVX2 instructions, but these are available on your machine and could speed up CPU computations.
W tensorflow/core/platform/cpu_feature_guard.cc:45] The TensorFlow library wasn't compiled to use FMA instructions, but these are available on your machine and could speed up CPU computations.
5.0
7.5
'''

在简单的数据网络这样可以很好地计算带正则化的损失函数，但是参数增多时，这样的方式可能导致损失函数的loss的定义很长，可读性差且容易出错。但更主要的是，当网络结构复杂之后定义网络结构的部分和计算损失函数的部分可能不在一个函数中，这样通过变量这种方式计算损失函数就不方便了。为了解决这个问题，可以使用TensorFlow中提供的集合(collection)。它可以在一个计算图中(tf.Graph)中保存一组实体(比如张量)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import tensorflow as tf


def get_weight(shape, ld):
    # 生成一个变量
    var = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
    # add_to_collection这个函数将这个新生成的变量L2正则化损失加入集合
    # 第一个参数是集合名字,第二个参数是加入的内容
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(ld)(var))
    # 返回生成的变量
    return var


x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
batch_size = 8
# 定义每一层网络中节点的个数
layer_dimension = [2, 10, 10, 10, 1]
# 数据网络的层数
n_layers = len(layer_dimension)
# 这个变量维护前向传播时最深的节点,开始的时候就是输入层
cur_layer = x
# 当前层节点个数
in_dimension = layer_dimension[0]
# 生成五层全连接的神经网络
for i in range(1, n_layers):
    # layer_dimension[i]:下一层节点个数
    out_dimension = layer_dimension[i]
    weight = get_weight([in_dimension, out_dimension], 0.001)
    bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
    # 使用ReLU
    cur_layer = tf.nn.relu(tf.matmul(cur_layer, weight) + bias)
    in_dimension = layer_dimension[i]

# 在神经网络前向传播时已经将所有的L2正则化损失加入了图的集合
# 这里只需要刻画模型在训练集上的损失函数
mse_loss = tf.reduce_mean(tf.square(y_ - cur_layer))
# 将均方误差损失函数加入集合
tf.add_to_collection('losses', mse_loss)
# get_collection返回一个列表,这个列表是所有集合中的元素
# 这个例子中这些元素就是损失函数的不同部分,将他们加起来就可以得到最终的损失函数
loss = tf.add_n(tf.get_collection('losses'))
Buy me a coffe. XD